
Yahoo Messenger is a well known name in Instant messenger category. After Windows Live Messenger it will be Yahoo Messenger to take position in favorite messenger list of users. Latest Yahoo Messenger available for download is Yahoo Messenger 9.0.0.2034.
Today while going thru Mininova Torrents I came across Yahoo Messenger 10 Final Torrent and I was totally surprised to see this since I am aware of latest Yahoo Messenger version which is 9.0.0.2034 and there is no news of Yahoo Messenger 10 under development. But then I thought this could be leaked Yahoo Messenger build.
Update: Download Yahoo Messenger 10 Beta Offline Installer
To confirm myself I started searching on Google and I saw couple of websites showing Yahoo Messenger 10 Final in search results, but most of the website in search results were warez one so it is difficult to believe this is true Yahoo Messenger 10 or some thing else, at the end to satisfy my curiosity I started downloading Yahoo Messenger 10.
Once I finished downloading Yahoo Messenger 10 first step I did was, install and check Yahoo Messenger build version. To my surprise it was “Yahoo Messenger For Vista Preview 2007.12.06.421”. Even shortcut for Yahoo Messenger on desktop says “Yahoo! Messenger for Vista”
Screenshots of Claimed Yahoo Messenger 10 Final

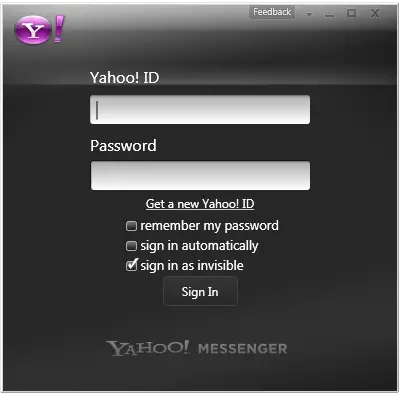
Yahoo has stopped development of Yahoo Messenger For Vista preview and only available Yahoo Messenger for Vista is Yahoo Messenger 9. It should be noted that last build number of Yahoo Messenger for Visa Preview was 1.2.1.1046.
But this Yahoo Messenger 10 raises some doubt whether its truly Yahoo Messenger 10 or its Yahoo Messenger for Vista Preview and if it’s Yahoo Messenger for Vista preview then why it is showing different build number (2007.12.06.421) then the last Build number (1.2.1.1046 Beta).
You can Download Claimed Yahoo Messenger 10 using below links
Download Yahoo Messenger 10 (Rapidshare)
Please Note : I am running Windows XP SP2 with Vista Transformation Pack so I am not sure Whether Yahoo Messenger For Vista Preview can be installed on Windows XP or not but this claimed Yahoo messenger 10 is working perfectly fine on Windows XP.


40 thoughts on “Yahoo Messenger 10 Final is Yahoo Messenger for Vista Preview ?”
hi! it is possible to run in my windows xp?
yes, i have istalled both (on XP SP2 and Vista). working perfect.
THANKSSSS
Tnx For the ym.
VERY NICE
i liked this siete only for downloading yahoo 10
Thnx a lot Bro.
It’s no good, you can’t open two chat windows at once ’cause the tabbing won’t work – gives it an error then forces it to close.
I have been install yahoo messenger 10, but i couldn’t login, I have no idea why?, I used Windows vista 64bit, anyone has any idea about this problem ?, help me please. I install yahoo messenger 9, its keep say unable to download files needed to installation, please check firewall setting and retry installation. But I already set off firewall.
Its so cool man
Dis contains virus it was detected by eset
THANKS & VERY NICE Yahoo Messenger is best instant messenger and provides many good features like PC to PC call
thanks, i try it
this is not Yahoo! Messenger 10. this version was being built long before Yahoo! Messenger 9.
thank u 4 tha yahoo
Thanks alot for this service
this isnt 10.0, this is just the Vista version they tried to make…..at least open it up before you write about it. its not a new version. this has been out for over a year now, yahoo just pulled the plug in the Vista version.
EPIC FAIL!!!
It was impossible to make a call by using yahoo messenger 10 for Vista
When is it really gonna come out??? is the download gonna be free???
Thanks dude for explaining!
hi everyone :) please tell why i can open two chat windows at once ??
theres a better version of beta 1.2.1046
works well
this is a preview
is there a web cam on yahoo messanger 10 and how to get it
TTTTTTTTTTTTTTTTTTHANKS
This stinks like the rest, have vista and this and all the others wont let me download say’s check firewall and retray please can anyone help me with this driving me crazy, I turn off firewall and still does the same thing ???????
I have dowloaded messenger 10 Beta on my laptop with Vista OS. Now I cannot make voice calls including all my contacts.
Why this happened?
When is it really gonna come out??? is the download gonna be free???
it is a verey good messanger and we all verey happy to know that you have made yahoo messanger 10 version new and we are happy.
Look i have vista 64 bit and have downloaded this version.. it sucks you cannot do webcam or view a webcam.. the pc to pc call is good though.. i have deleted it adn reinstalled the messenger 9 works great no problems whatsoever so dont even bother downloading the messenger 10 or beta or preiview just the 9….
here is the link to it
http://messenger.yahoo.com/download
have fun
Daniel
i like yahoo messenger very like yahoo
In addition, Y! Updates support Twitter and YouTube, which isn’t much of a feature really, considering the stuff they don’t have implemented. The only positive thing that Yahoo Messenger 10 has over v9 is the modding part itself, where all parts of the UI/language files are editable in Resource Hacker.
dose this replace yahoo 9
i found a newhome with this latest version
THanx…………………
thanku dude
thanks for yahoo 10
kos
please open it
thaaaaanx
With MILLIONS of Vista programs out “there”, Yahoo needs to get it’s **** together and correct (THEIR) problems and compatibility issues with the Vista program.